Nim : A1C219011
Kelas : R-001
Dosen Pengampu: NOVA SUSANTI, S.Pd .,M.pd
Pendidikan matematika universitas Jambi
1. Pembuktian kecepatan sesaat
Kecepatan sesaat adalah kecepatan rata-rata pada limit selang waktu Δt mendekati nol. Secara matematis kecepatan sesaat dituliskan:
dx/dt adalah turunan pertama fungsi vektor posisi terhadap waktu.
jika r = xi + yj dan Δr = Δxi + Δyj
maka :
dengan:
v = vektor kecepatan sesaat (m/s)
νx = dx/dt komponen kecepatan sesaat pada sumbu x (m/s)
νy = dy/dt komponen kecepatan sesaat pada sumbu y (m/s)
Arah kecepatan sesaat merupakan arah garis singgung lintasan di titik tersebut.
Berdasarkan persamaan kecepatan sesaat berikut :
kecepatan dapat dicari dengan turunan dari fungsi posisinya. Sebaliknya, jika fungsi kecepatan diketahui, fungsi posisi dapat ditentukan dengan mengintegralkan fungsi kecepatan tersebut
v = dr/dt
dr = v.dt
Apabila persamaan tersebut diintegralkan, maka:
dengan :
r0= posisi awal (m)
r = posisi pada waktu t (m)
v = kecepatan yang merupakan fungsi waktu (m/s)
Komponen posisi pada arah sumbu x dan sumbu y adalah :
2 . percepatan sesaat
Percepatan sesaat didefinisikan sebagai limit kecepatan rata-rata untuk interval waktu mendekati nol.
jka v = vx i + vy j , maka :
a = axi + ayj ......(4)
dengan :
a = vektor percepatan
Dari persamaan (4) dapat dikatakan bahwa percepatan merupakan turunan dari fungsi kecepatan terhadap waktu. Percepatan juga merupakan turunan kedua fungsi posisi terhadap waktu.
Percepatan sesaat merupakan kemiringan grafik kecepatan terhadap waktu.
Kerena:
maka persamaan (4) dapat dituliskan:
Sehingga percepatan sesaat menjadi :
3.
Berdasarkan gambar tersebut Berapa tegangan tali?
Jawaban:
Diketahui: “α” = 37° β “= 53° W = 4 N
Tinjau T3 :
∑ fy = 0
T3-W =0
T3 = W
T3 = 4N
Tinjau T1 dan T2
∑fx = 0
T2x- T1x = 0
T2x = T1x
T2.cos 53 = T1.cos 37
T2. 0,6 = T1. 0,8
T2 = T1. 0,8/ 0,6
T2 = T1. 4/3
T2 = 4/3 T1
∑fy =0
T1y + T2y -T3 = 0
T1y+T2y =T3
T1.sin 37° + T2. Sin 53° = 4
T1. 0,6 +T2. 0,8 =4
0,6 T1 +4/3 T1.0,8 =4
6/10. T1 + 4/3 T1. 8/10 =4
3/5 T1 + 16/15 T1 =4 x15
9T1 +16 T1 =60
25T1 =60
T1 =60/25
T1 = 2,4 N
Selanjutnya substitusi kan
T2= 4/3 T1
T2= 4/3. 2,4
= 3,2 N
4.
Berapakah resultan gaya?
Diketahui :
F1: 4N, F2: 4N, F3: 6N
Sin 45°=½√2=0,7;cos 45°=½√2=0,7
Sin 30°=cos 60°=½=0,5
Cos 30°=sin 60°=½√3=0,9
Arah resultan melalui sumbu x
ƸFx=F1cos 45°+F3cos 60°-F2cos30°
= 4(0,7)+6(0,5)-5(0,9)
= 2,8 + 3 - 4,5
= 1,3 N
Arah resultan melalui sumbu y
ƸFy=F1sin 45°+F2sin 30° –F3sin60°
= 4(0,7)+ 5(0,5)-6(0,9)
= 2,8 +2,5-5,4
= - 0,1 N
R=✓(ƸFx)2+(ƸFy)2
= ✓(1,3)2+(-0,1)2
= 1,303

















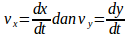


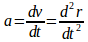




Tidak ada komentar:
Posting Komentar