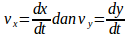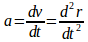Nim : A1C219011
Kelas : R-001
Prodi : pendidikan matematika
Mata kuliah : fisika dasar
UJIAN TENGAH SEMESTER
1. Benda A massa 3kg terletak pada bidang miring ditarik dengan gaya sebesar 4 N, jika benda B bermassa 4kg dihubungkan dengan benda A dan digantung vertikal dengan sebuah katrol (a) tentukan percepatan masing – masing benda (b) tentukan tegangan tali, jika diketahui percepatan gravitasi 10 m/s2 dan koefisien kinetiknya 0,1 ?
2.Pada gerak suatu partikel sepanjang garis lurus, grafik kecepatan v terhadap waktu t dapat dilihat dari gambar berikut ini :
a. Berapakah percepatan partikel pada saat – saat t = 2s, 4s, 8s, 10s
b.B panjang lintasan yang ditempuh partikel dalam selang waktu antara t = 0 dan t = 10 s
c. Berapakah perpindahan partikel pada selang waktu tersebut
d. Berapa kecepatan rata – rata partikel dalam selang waktu t = 2s dan t = 8s
3. Sebuah benda bermassa 5kg dengan kecepatan 3m/s bertumbukan dengan benda yang bermassa 10kg dengan kecepatan 2m/s. Setelah terjadi tumbukan benda bermassa 10kg kecepatannya menjadi 4m/s dan bergerak searah dengan arah gerak sebelum tumbukan (a) tentukanlah kecepatan benda bermassa 5kg setelah tumbukan (b) tentukan besar perubahan total energi kinetik benda yang bertumbukan ?
4. A. Vektor A : 3i + j -3k
Vektor B : 2i -5j + 2k
Vektor C : -i + 2j -6k
Hitunglah : a. (A . B) x C
b. A .( B + C)
c. A x (B + C)
B. Carilah dimensinya :
Kecepatan
Usaha
Tekanan
Inpuls
Momentum
5. Sebuah balok didorong oleh gaya mendatar F yang membuat sudut 37⁰ dengan garis mendatar, seperti gambar dibawah ini. Massa balok 2 kg bergerak dengan kecepatan konstan, koefisien gesekan kinetik antara balok dengan lantai adalah 0,2. Tentukan usaha yang dilakukan oleh gaya jika balok didorong sejauh 20 m
6. Sebuah benda bergerak sepanjang garis lurus dengan persamaan geraknya
X = 16t2 + 6t+3
a.kedudukan benda pada t = 2
b.Bilamanakah benda melewati titik asal
c.Hitunglah kecepatan rata – rata pada selang waktu 0 < t < 2 detik
d.persamaan umum kecepatan rata – rata pada selang waktu antara to dan (to + Δt)
e.kecepatan seketika pada setiap saat
f.Tentukan kecepatan seketika pada t = 0
g.Bilamanakan dan dimanakah kecepatan sama dengan nol
h.Tentukan persamaan umum percepatan rata – rata pada selang waktu antara to < t < (to + Δt)
i.Tentukan persamaan umum percepatan seketika pada setiap saat
j.Bilamanakah percepatan seketika sama dengan nol
k.Gambarkan grafik – grafik x, v dan a masing – masing sebagai fungsi waktu
7. Air keluar dari selang dengan debit 2,5 kg/s dan lajunya 25 m/s dan diarahkan pada sisi mobil, yang menghentikan gerak majunya. Abaikan percikan air kebelakang, berapakah gaya yang diberikan air pada mobil jika besarnya gaya tersebut adalah perubahan momentum terhadap perubahan waktu ?
8. pistol ditembakan vertikal ke balok kayu 1,4kg yang sedang dalam keadaan diam persis diatasnya. Jika peluru memiliki massa 21 gram dan laju 210 m/s, seberapa tinggi balok tersebut akan naik setelah peluru tertaman di dalamnya ?
Jawab :
1.
Diketahui :
2. A. t=2s, a = Δv/Δt
a = 20-0 / 2-0 = 10 m/s²
t=4s, a = 20-0/ 4-0 = 5m/s²
t=8s, a= 20-0/8-0. = 2,5 m/s²
t= 10s, a= 20-(-10)/10=3 m/s²
B. a = 10m/s²
=> -10 = -10-0/ R-8
-10 = -10/R-8
R-8 = -10/10
R. = 9
L trapesium 1 = 1/2 (a+b) t
= 1/2 ( 12) 20
= 120 m
L trapesium 2 = 1/2 ( 2 + 1) (-10)
= -15 m
L1 + L2 = 120 m + (15)m
= 135 m
C. Perpindahan = 120- 15
= 105 m
D. V rata rata = perpindahan / total waktu
= 105 / 6
= 17,5 m/s